• View
• Edit
• History
• Print

OperationsWithSets

Geometric operations with convex sets

• Methods for determining basic properties
• Working with multiple sets
• Geometric methods
  • Set containment
  • Distance to a point
  • Project a point onto the set
  • Separation hyperplane
  • Extreme points
  • Support
  • Ray shooting
  • Outer approximation using a bounding box

Methods for determining basic properties of sets

Consider the following example where the set is built from the following constraints

It is very often of interest to check wheter the set is empty or not. In MPT there exist an isEmptySet method that checks whether the set is empty

Another useful property is boundedness which can be checked using the isBounded method, i.e.

These properties can be veriefied by plotting the set using plot method

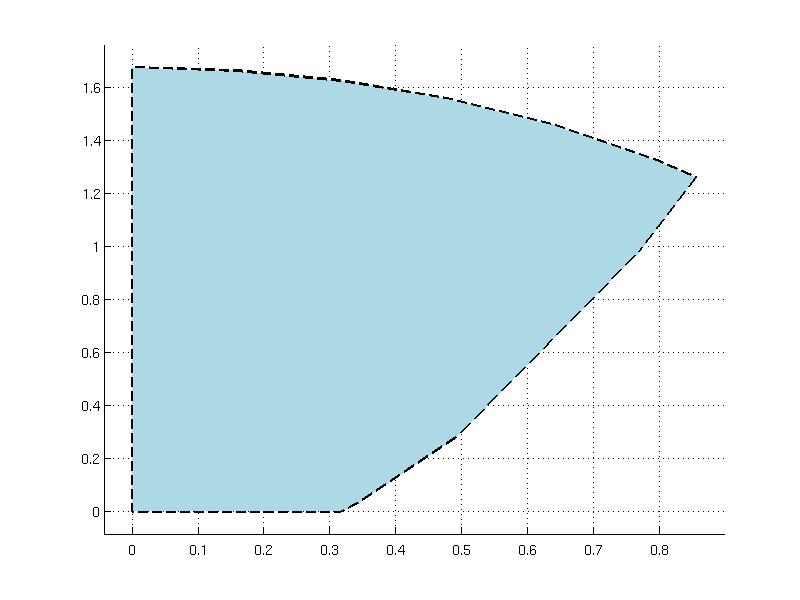
Note that plotting of general convex sets could become time consuming because the set is sampled with an uniform grid. The value of the grid can be changed using the grid option of the plot method, for details type

Working with multiple sets

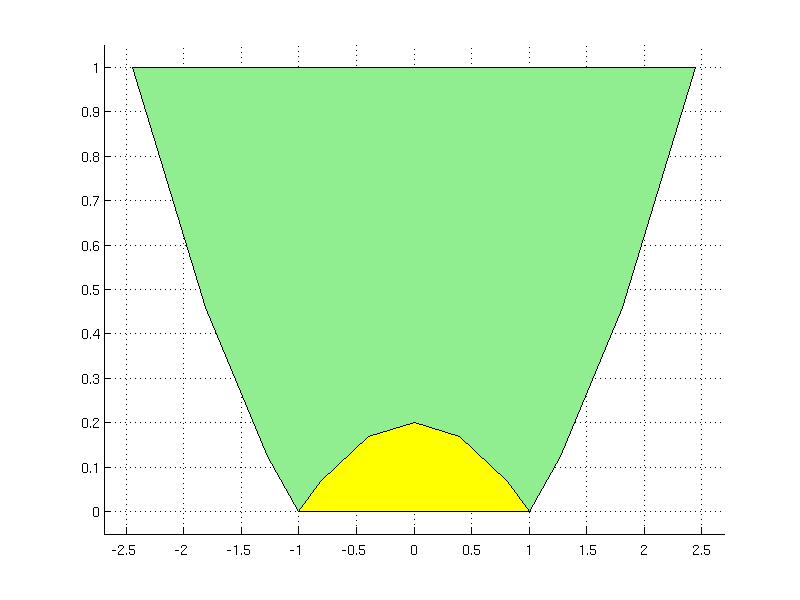
Consider following two sets created with the help of YALMIP

which are plotted in different colors

The above sets can be concatenated into an array using overloaded [ ] operators. The column concatenation can be done using brackets or vertcat method which are equivalent:

The row concatenation using brackets or horzcat method

If the sets are stored in an array, some methods can operate on the array, for instance

If the method is not applicable on the array, it can be invoked for each element in the array using forEach method:

The forEach method is a fast replacement of for-loop and it can be useful for user-specific operations over an array of convex sets.

To create a new copy of the ConvexSet, the copy must be employed, otherwise the new object points to the same data stored in the original object

Geometric methods

The ConvexSet class offers a couple of methods for use in computational geometry. Consider a following set which is created as an intersection of quadratic and linear constraints

which is plotted in salmon color

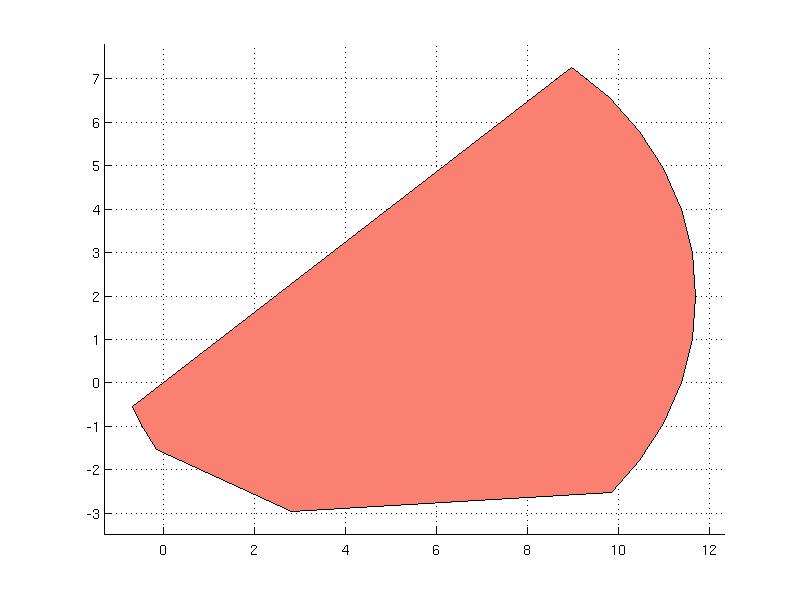
This set will be used next to demonstrate some methods that can be applied to YSet objects.

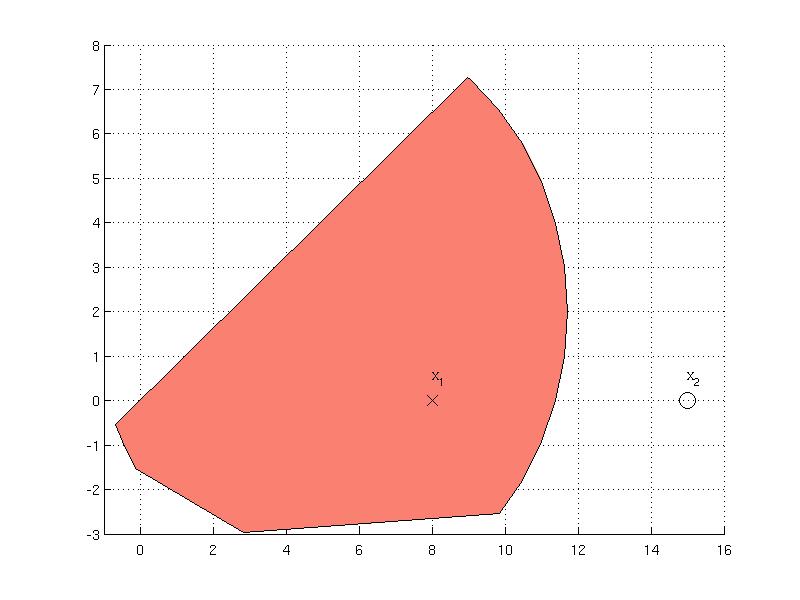
Set containment test

To check if the point is contained in the set or not, there exist a method contains. For instance, the point x1=[8; 0] lies in the set

but the point x2 = [15; 0] lies not:

Distance to a point

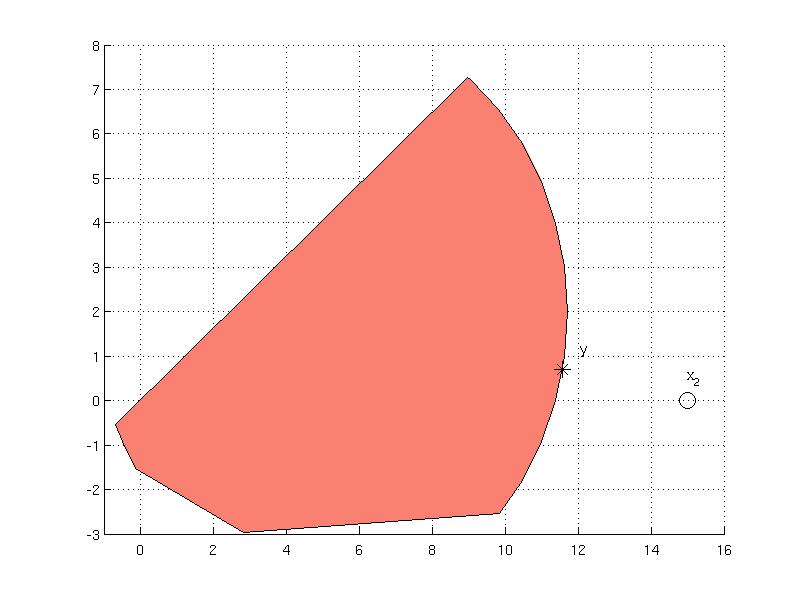
Computing distance from the set to a given point is achieved using distance method. For instance, the distance to the point x2 that lies outside of the set S can be computed as follows

The output from the method is a structure with four fields indicating the result of the computing the distance. The field exitflag indicates the exit status from the optimization solver, the actual distance is available in dist field and fields x, y indicate the coordinates of the two points for which the distance has been computed. It can be extracted from the field y which point is the closest to the point x2 and plotted.

Point projection onto a set

Computation of the distance is achieved also in the project method which computes the closest point to the set. For the point x2 the projection operation results in a structure with four fields

The field exitflag informs about the status returned from the optimization solver which can be found also in the how field. The closed point is computed in x field and the value about the distance can be found in dist field. One can verify that the computed point by the projection operation is the same as by distance operation

Separation hyperplane from a point

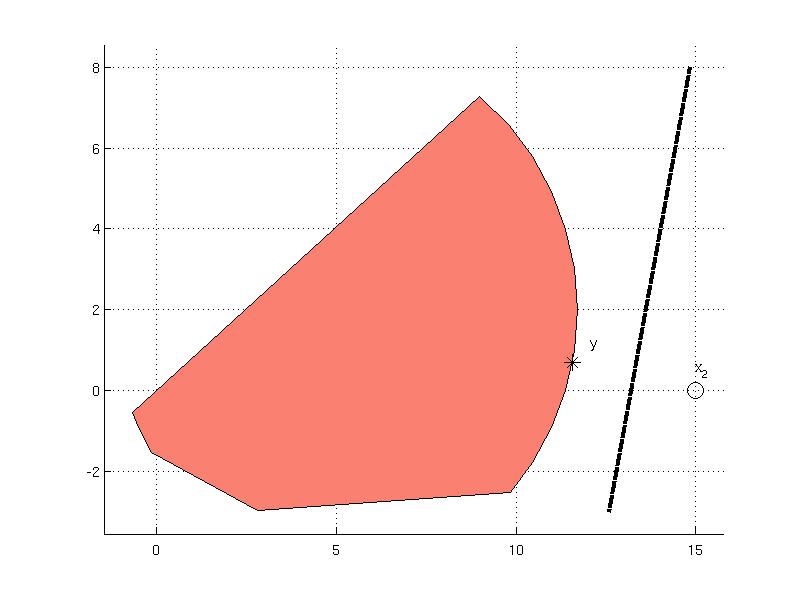
The YSet object implements the separate method that computes a hyperplane that separates the set from a given point. As an example, consider computation of a separating hyperplane from the set S and the point x2:

which returns a data corresponding to a hyperplane equation { x | He*[x; -1] = 0 }. To plot the computed hyperplane, a Polyhedron object is constructed

and plotted.

Extreme point in a given direction

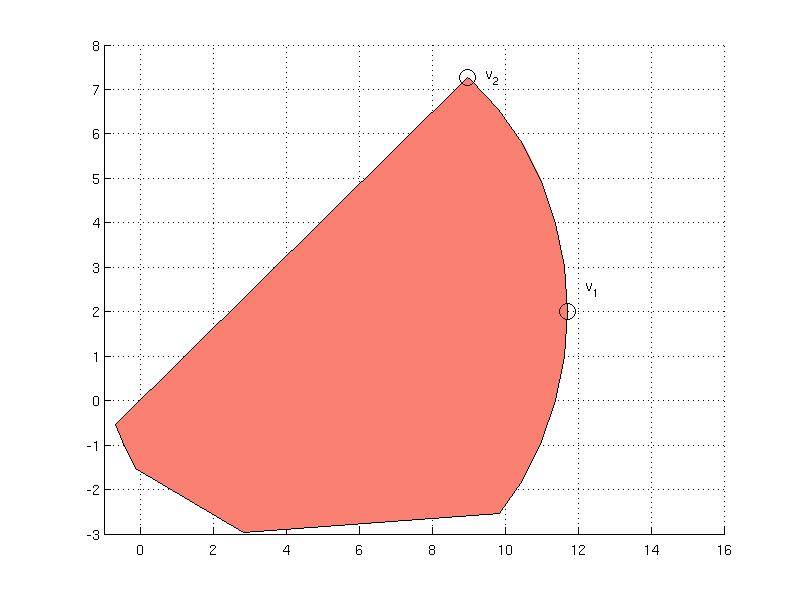
Computation of extreme points for a convex set is implemented in the extreme method. The method accepts a point as an argument that specifies the direction in which to compute the extreme point. For instance, for the point x2, the extreme method results in

The output variable v1 contains the status returned from the optimization solver in exitflag and how fields. The extreme point is stored in x variable and the field supp corresponds to a support of the set given as { max x'*y s.t. y in Set }. The extreme point in the direction x3 = [0; 5] is given as

One can visually inspect the location of the computed extreme points v1.x and v2.x in the figure below:

Computing a support of the set in a given direction

For a given point x, the support of a set is given as { max x'*y s.t. y in Set }. This feature is implemented in the support method. The syntax of the support method requires a point x which determines the direction and the value of the maximum over the set is returned.

Note that computation of the support is available also in the extreme method.

Maximum over the set in a given direction - ray shooting

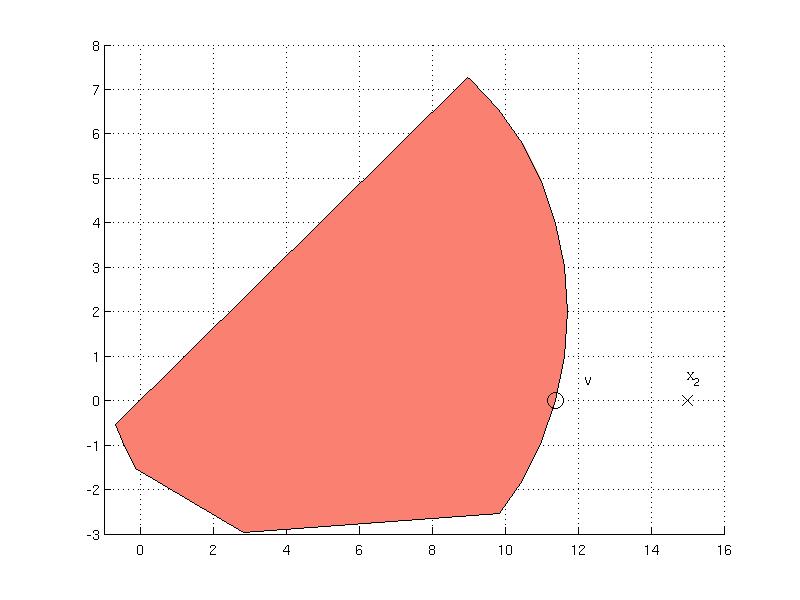
The ray-shooting problem is given by { max alpha s.t. alpha*x in Set } and is available in the shoot method. As an example, consider computation of the maximum of the set in the direction of the point x2 = [15; 0] which gives the value of alpha

Multiplying this value with the point x2 one obtains the point v = alpha * x2 that lies on the boundary of the set

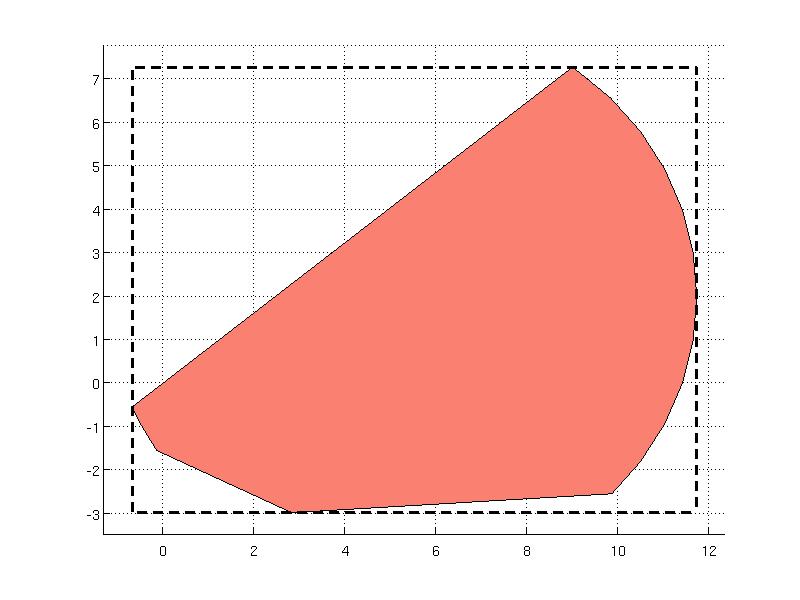
Outer approximation

Computation of the bounding box over the set is implemented in outerApprox method:

The method returns a polyhedron with lower and upper bounds that are stored internally and can be accessed by referring to Internal property

Comparison of the bounding box B wih the orignal set S can be found on the figure below which was generated with the following command:

Back to Computational Geometry overview.